#1978 소수 찾기

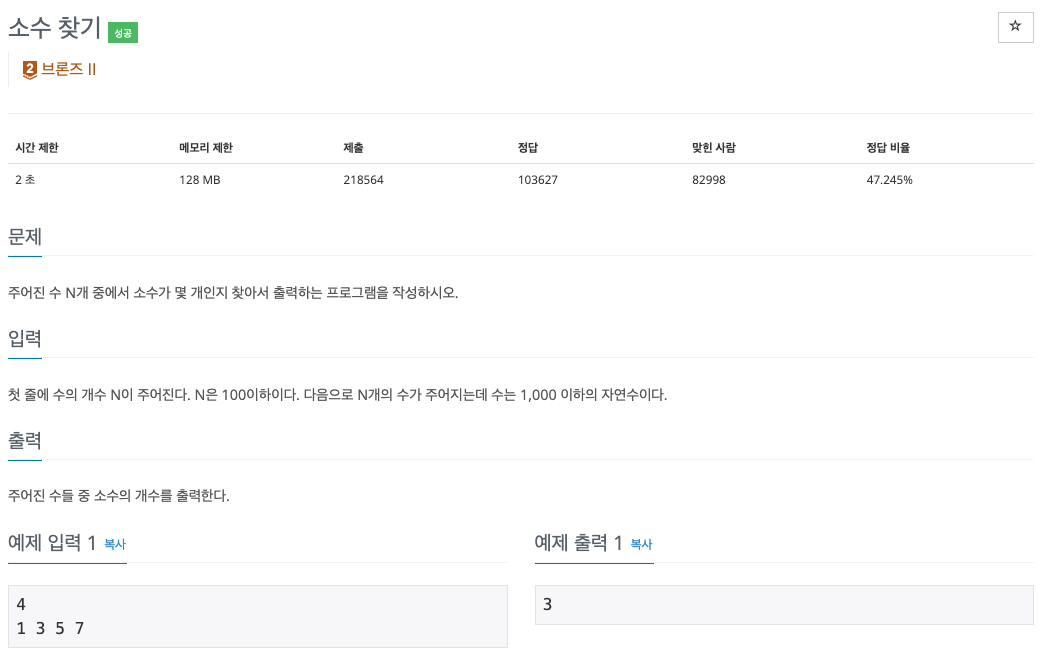
문제

---

 

코드

---

import kotlin.math.sqrt

fun main() = with(System.`in`.bufferedReader()) {
    readLine()
    val num = readLine().split(' ').map { it.toInt() }
    val prime = BooleanArray(1001) {true}
    prime[0] = false; prime[1] = false
    for (i in 1..sqrt(1000f).toInt()) { // 특정 숫자의 제곱근까지만 확인하면 됨
        if (!prime[i]) continue
        for (j in i * i .. 1000 step i) {  // i의 제곱부터 시작하면 됨
            prime[j] = false
        }
    }
    var count = 0
    for (e in num) {
        if (prime[e]) count++
    }
    println(count)
}

아래 풀이를 보면 주석에 대해 이해할 수 있을 것!!

 

풀이

---

에라토스테네스의 체에 대해 다시 한 번 공부했다.

 

에라토스테네스의 체

1. 2부터 N까지의 자연수를 나열
2. 남은 수 중에서 제거되지 않은 가장 작은 수 i를 찾음
3. 남은 수 중에서 i의 배수를 모두 제거한다
4. 2번과 3번 과정을 반복

 

에라토스테네스 체의 중요한 특징

• 특정 숫자의 제곱근까지만 검토하면 된다
  • 왜냐하면 n의 경우 제곱근 n보다 큰 약수가 존재한다면, 이미 그 보다 작은 약수와 짝을 이뤘기 때문
  • 예를 들어 n이 36이라고 하자.
  • 1, 36 / 2, 18 / 3, 12 / 4, 9 / 6, 6 / 9, 4 / 12, 3 / 18, 2 / 36, 1
  • 이런 식이기 때문에 6, 6을 기준으로 동일한 pair를 이룸
  • 따라서 36의 제곱근인 6보다 큰 약수인 9, 12, 18, 36은 이미 6보다 작은 약수 4, 3, 2, 1과 짝을 이뤘기 때문에
  • 제곱근인 6까지만 확인해 보면 됨
• i의 배수를 제거하는 과정에서 i의 제곱부터 시작하면 된다
  • 만약 i가 5라면, 5의 배수는 이미 2, 3, 4의 배수에서 제거되었기 때문에 5의 제곱부터 시작하면 된다

 

참고

https://ko.wikipedia.org/wiki/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98_%EC%B2%B4